Daftar Masuk

Arsip

Gudang Soal Fisika - SMA/MA OSP Fisika 2018 Soal Nomor 3

Soal No. 3

(13 poin) Tinjau sebuah batang tipis bermassa m1 dengan panjang 4L yang dapat bergerak bebas diatas bidang horisontal (bidang xy) licin. Batang tipis mula-mula hanya berotasi terhadap pusat massanya 0 dengan kecepatan sudut \omega1 berlawanan arahjarumjam (jika dilihat dari atas). Anggap 0 adalah pusat koordinat xy. Sebuah partikel bermassa m2 bergerak mendekati batang dengan kecepatan v2 sejajar sumbu y denganjarak L (pada garis x = -L) ke arah y positif (lihat gambar dibawah). Pada saat tumbukan terjadi, batang membentuk sudut 45° terhadap sumbu x negatif. Sesaat setelah tumbukan, m2 bergerak ke kiri searah sumbu x negatif. Tumbukan bersifat lenting sempurna. 
a. Tentukan persamaan-persamaan yang memenuhi peristiwa tumbukan. 

Untuk selanjutnya, gunakan kasus khusus m1 = m2 dan v2 = \omega1L.
b. Tentukan kecepatan m1, kecepatan m2 serta kecepatan sudut m1 setelah tumbukan.

Muhammad Hanif Yaqub
At 26-Feb-2023 02:13

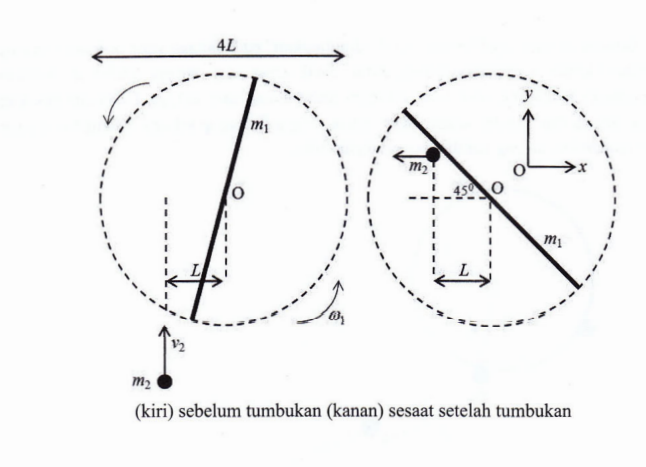
a. Pada saat tumbukan, terdapat hukum kekekalan momentum dan hukum kekekalan energi kinetik. Mari tuliskan persamaan-persamaan yang memenuhi peristiwa tumbukan:

Hukum kekekalan momentum: m1 * v1 = m1 * v1' + m2 * v2'

Hukum kekekalan energi kinetik: 1/2 * m1 * v1^2 = 1/2 * m1 * v1'^2 + 1/2 * I1 * \omega1'^2 + 1/2 * m2 * v2'^2

dengan I1 adalah momen inersia batang tipis terhadap sumbu tengahnya dan \omega1' adalah kecepatan sudut batang tipis setelah tumbukan.

b. Diketahui m1 = m2 = m dan v2 = \omega1L. Dalam kasus ini, momen inersia batang tipis terhadap sumbu tengahnya adalah I1 = (1/12) * m * (4L)^2 = (1/3) * m * L^2.

Mari selesaikan persamaan-persamaan di atas untuk mencari kecepatan m1, kecepatan m2, dan kecepatan sudut m1 setelah tumbukan:

Hukum kekekalan momentum: m * v1 = m * v1' + m * v2' v1 = v1' + v2'

Hukum kekekalan energi kinetik: 1/2 * m * v1^2 = 1/2 * m * v1'^2 + 1/2 * I1 * \omega1'^2 + 1/2 * m * v2'^2 1/2 * m * (v1' + v2')^2 = 1/2 * m * v1'^2 + 1/2 * (1/3) * m * L^2 * \omega1'^2 + 1/2 * m * v2'^2 1/2 * m * (v1'^2 + 2 * v1' * v2' + v2'^2) = 1/2 * m * v1'^2 + 1/2 * (1/3) * m * L^2 * \omega1'^2 + 1/2 * m * v2'^2 1/2 * m * v1'^2 + 1/2 * m * v2'^2 + 1/2 * (1/3) * m * L^2 * \omega1'^2 = 1/2 * m * (v1'^2 + v2'^2)

Substitusi v1 = v1' + v2' ke dalam persamaan kekekalan momentum memberikan: m * (v1' + v2') = m * v1' + m * v2' v1' = (m - m2/m) * v2'

Substitusi v1' ke dalam persamaan kekekalan energi kinetik memberikan: 1/2 * m * ((m - m2/m) * v2')^2 + 1/2 * m * v2'^2 + 1/2 * (1/3) * m * L^2 * \omega1'^2 = 1/2 * m * ((m - m2/m) * v2')

About

Forum dan Kelas Online ini disediakan untuk diskusi soal, mengakses materi dan media program jarak jauh yang ditunjukkan bagi Partisipan Olimpiade Sains dari seluruh daerah se Indonesia
Legalitas dan Izin Usaha :
NIB : 30112300XXXXX
No Pendaftaran Merk : IDM001122612
AHU-0242267.AH.01.11 Tahun 2023

Our Social Media

Facebook  Twitter  Google  Instagram  Youtube 
© 2025 PT. Pelatos Nasional Indonesia